Carnot Cycle – Principles and Calculations

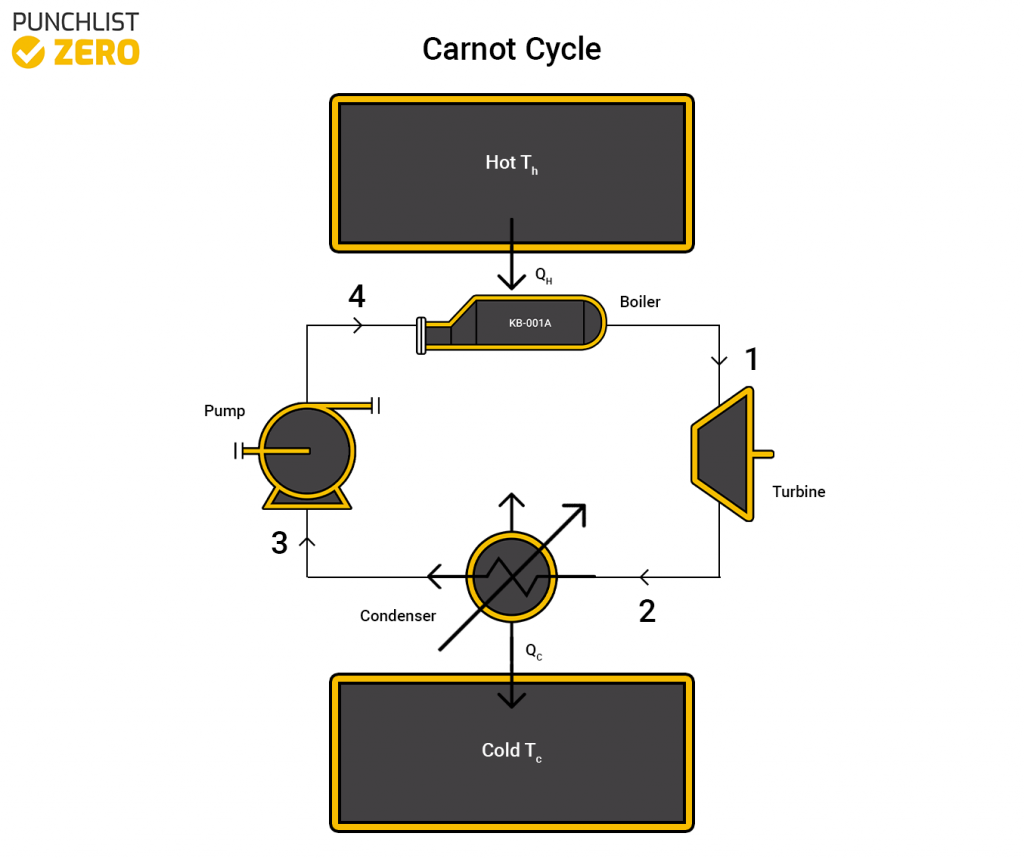
The Carnot cycle is a thermodynamic cycle that represents a theoretical heat engine. The main reason why the cycle can not actually exist is that the concept relies on holding a 100% efficiency. In the real world friction and heat loss occurs, thus making it impossible to achieve perfect efficiency. In this article, you will learn the principles, calculations, and uses of the Carnot cycle.

Principles of the Carnot Cycle

The Carnot cycle starts with an isothermal expansion where heat transfers from a hot reservoir at a constant temperature. Along with the heat transfer, a reversible pressure drop occurs. Next, an isentropic expansion occurs, reducing the pressure of the system and causing the temperature to drop to that of the cold reservoir. The cold reservoir ideally rests at absolute zero, implying perfect efficiency.

In the next stage, an isothermal compression happens, where the heat transfers to the cold reservoir without a temperature change. This also occurs reversibly, meaning that the entropy change into the system is the same as out of it. Finally, an Adiabatic compression occurs where the pressure raises until the temperature of the gas reaches that of the hot reservoir.

With these implications in place, a diagram of temperature vs entropy equals a perfect square, implying complete reversibility.This cycle in reverse no longer represents a heat engine but turns into a perfect efficiency Carnot refrigeration cycle. As the cycle is theoretical, we can use the cycle to represent and compare it to other cycles. We can use the temperature values of real cycles to find ideal efficiencies in terms of a Carnot cycle.

Calculations of the Carnot Cycle

Representing another cycle within the Carnot cycle is one of its main uses. By knowing the maximum(Th) and minimum(Tc) temperature which occur in the other cycle allows the determination of idealized efficiency(ηT).

   

With either the heat input(Qin) or work done(Wout) known, the other can be found simply.

   

   

Using the found efficiency allows comparison to another cycle. The efficiency of the Carnot cycle will be the ideal perfect efficiency possible by the given temperature range. This may then maximize cycles in the most efficient way given their temperature ranges.

Uses of the Carnot Cycle

The Carnot cycle can only be described as a baseline cycle. Because of its issues with the perfect efficiencies, there is no plausible way the cycle could exist. However, the cycle still serves a useful purpose. Using it to compare to and contrast newly developed cycles that may not hold perfect efficiencies but can better utilize higher concentrated fuels and temperature variation.

The concept of the Carnot cycle is what drove the world to the modern thermodynamic cycles we have today. In fact, the cycle’s concepts help develop better versions of engines to this day.

The Carnot cycle has also helped discover other principles and concepts in thermodynamics that make what we have today possible. Studying of the cycle led to the development of a thermodynamic concept called entropy. It also led to the concept that any fluid capable of expansion may operate as a working fluid of a thermodynamic cycle. Substances such as water, air, and R-134a became common fluids to use within cycles from this research.

Heat engines are the most common application. They occur in all sorts of different larger vehicles such as airplanes, boats, and trains. There are also heat pumps that also root from the cycle. They see use in heating applications such as refrigerators or HVAC units.

History of the Carnot Cycle

The Carnot cycle was developed by a French engineer named Nicolas Léonard Sadi Carnot in 1824. Known widely as the “father of thermodynamics” his original concepts spawned the ability for engines to exist as they do today. His work gave later scientists a foundation to better define laws of thermodynamics. Among those was Rudolf Clausius and his mathematical work on the model. This work done with the Carnot cycle lead to the modern airplane engine and modern train engines.

Throughout time, the idea behind the Carnot cycle has shifted slightly to adapt to modern applications. Where its original design used a piston, now the cycle uses any sort of heat engine. However, in actual applications, these cant have perfect efficiency. In modern times the Carnot cycle provides a baseline comparison on what the maximum output of a system would be.