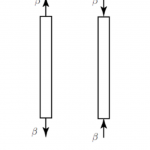
The modulus of rigidity is the ratio of shear stress to shear strain. Thus, it measures the ability of the material to withstand distortion. However, the rigidity of the material varies at different temperatures and pressures. The main value of the modulus of rigidity is a description of the material hardness and insight into the point where material deformation occurs. In this article, you will learn the modulus of rigidity equation, its applicability to steel, and common values.
Modulus of Rigidity Equation
The Modulus of rigidity(G), which is sometimes referred to as the shear modulus, can be calculated simply by shear stress(τxy) over shear strain(γxy).
![]()
Shear stress may be expanded into force(F) over the area(A) where the force acts. Shear strain may also expand into the transverse displacement(Δx) over the initial length of the area(l).
![]()
There are also models that exist to predict this number for different metals, alloys, and plastics. These take into account temperature, pressure, and other factors to determine how the modulus of rigidity changes with the variation of these factors.
The MTS Model
The MTS model is used mainly for plastics. This specific model only uses temperature and not pressure. The model takes in a few different variables to work, such as the shear modulus(μ0) when the temperature(T) is at 0K, and the flexural rigidity(D).
![]()
The SCG Model
Another model is the SCG(Steinberg-Cochran-Guinan) model, a pressure dependent model. This model accounts account for density(ρ), pressure(p) and temperature(T). The modulus of rigidity(μ0) is considered at (T = 300K, p = 0, η = 1).
![]()
Where:
![]()
The NP Model
The last commonly used model is NP(Nadal-Le Poac) which is a variation of the SCG model. NP swaps the temperature dependence of the SGC for a part based on the Lindemann melting theory. Variables are temperature(T), pressure(p), the Lindemann constant(f), the atomic mass(m), and a material parameter(ζ). The modulus of rigidity(μ0) is considered at (T = 0K, p = ambient pressure).
![]()
Where:
![]()
![Rendered by QuickLaTeX.com \[ \jmath(\hat{T}) := 1 + exp (- \frac{1 + \frac{1}{\zeta}}{1 + \frac{\zeta}{1 - \hat{T}}}) \]](https://punchlistzero.com/wp-content/ql-cache/quicklatex.com-33984b2355638ccca0d8971ee18e496f_l3.png)
![]()
Modulus of Rigidity of Steel
The modulus of rigidity for steel is around 79 GPa or 11,460 ksi. This value gives steel one of the highest values of commercially available metals.
The importance of modulus of rigidity to material selection depends on the item’s application. If the material needs to hold or brace a component, aim for a modulus of rigidity that provides a good deal of safety factor. If the material serves as a covering, accessory, and not the main load-bearing member, the modulus of rigidity may be closer to the theoretical max force it will receive.
Generally speaking, steel strength ranges from 36ksi to 50ksi. Depending on the applications, higher strength alloys may be specified. As strength increases, so does expense. For this reason, solving for the minimum shear modulus keeps costs to a minimum and allows users to select the most economical and effective alloy.
It is also important to consider steel formation and the orientation of the material. For instance, a plate’s grain direction results from a mill’s rolling process and stretches the metallurgical structure. A material’s bending ability fluctuates with and against the grain.
Common Values in Everyday Materials
Understanding everyday material values provides insight during the material selection process. General modulus of rigidity values are represented below. A high value means the material maintains its shape and large force is required to deform it. A low value means the material is more flexible. Liquids generally have a modulus of rigidity value of 0 as any applied force induces deformation.
| Material | Modulus of Rigidity Value (GPa) |
| Aluminum | 26 |
| Brass | 41 |
| Invar | 56 |
| Iron | 82 |
| Lead | 5.6 |
| Magnesium | 17 |
| Steel- A36 | 79.3 |
| Steel (Cold-Rolled) | 79 |
| Titanium(Grade 2) | 45 |
| Zinc | 43 |